[논문리뷰] Filter Pruning via Geometric Median for Deep Convolutional Neural Networks Acceleration

1. Introduction and Motivations

Filter pruning은 선택된 필터를 직접 제거하는 방법과 제거 하지 않고 가중치를 0으로 변경하여 구조는 유지하면서 가중치는 제거하는 방법이 있다. Hard pruning의 문제점을 해결하고자 Soft pruning 방법을 제안한 논문이 등장했다. 이 방법은 “Smaller-norm-less-important”의 기준에 따라 l2-norm값이 작은 필터를 제거하되 완전히 제거하는 것이 아니라 일정 에폭 이후에 가중치를 다시 update한다.

하지만 “Smaller-norm-less-important” 기준에서 중요한 가정이 있다; 1) 필터의 norm 분산이 충분히 커야하고, 2) 제거하고자 하는 norm이 충분히 작아야한다는 점이다. 다시말해 norm이 상대적으로 작지만 높은 기여를 하고 있으면 안되고, 납득할 수 있을 정도로 충분히 작아서 기여도가 적다고 판단할 수 있어야한다. 모델 pruning은 위의 조건을 이상적으로 고려하고 진행하지만 현실적으로 위와 같은 조건을 항상 만족하는 것은 아니다.

따라서 본 논문에서는 가장 기여도 교체가 가능한(Most replaceable contribution) 필터를 선택하는 FPGM(Filter Pruning via Geometric Median)기법을 제시한다. 이 방법은 같은 layer에 있는 필터들의 Geometric Median(GM) 값을 계산하여 GM 값 근처에 있는 필터들은 서로가 비슷한 특징을 포함하고있다고 생각하여 제거하는 방식이다.

여기서 오해하지 말아야할 점은 Large norm filter가 많은 지역을 바탕으로 제거하는것이 아니라, 기하학적(Geometric) 위치를 바탕으로 제거하는 것이다. 아래 그림이 오해소지가 좀있는데, 마치 Large norm이 세개라서 하나를 제거한 것처럼 해석할 수 있지만 사실은 GM 값을 minize하기 위한 필터가 제거된 것이다.

 

2. Methodology

2.1 Analysis of Norm-based Criterion

앞서 언급했든 norm을 기준으로 pruning을 하는 것이 항상 훌륭한 결과를 보이는 것은 아니다. 두 가지 조건을 만족해야한다; 1) Deviation of filter norms should be significant. 2) The norms of those filters which can be pruned should be arbitrarily small.

Small Norm Deviation. Figure 2(a)의 그림을 보면 이상적인 norm devivation이 파란색이라고 할때, 실제 환경에서는 초록색과 같은 상황이 나타날 수 있다. 이런 경우 pruning을 위한 threshold를 정하는 공간(search space)가 작기 때문에 제대로된 기준으로 활용하기 어렵다.

Large Minimum Norm. Norm 값이 0에 가까워야 해당 필터를 제거하는것이 전체 성능에 영향을 미치지 않는다라고 판단 할 수 있다. Figure 2(b)를 살펴보면 파란색 dash line 처럼 0에 norm의 분포가 0에 가까워야 한다.하지만, 실제 환경에서는 초록색 부분과 같이 0에서 먼 분포를 갖고 있을 수 있다. 이런 경우 상대적으로 small norm을 삭제하는것이 전체 모델에 약영향을 미칠 수 있다.

2.3 Filter Pruning via Geometric Median

Norm-based criterion의 단점을 극복하기 위해서 논문의 저자들은 geometric median을 활용한 제거법을 제시한다. 주요 idea인 geometric median은 다음과 같다: 주어진 $n$ 개의 포인트 $a^{(1)},...,a^{(n)}$ with each $a^{(i)}\in {\mathbb{R}}^d$, Euclidean distance를 최소화 할 수 있는 한 점 $x^{\ast }\in {\mathbb{R}}^d$ 를 찾는 것.

$$x^{\ast }\in \underset{x}{\mathrm{argmin}}f(x)wheref(x)\stackrel{def}{=}\sum _{i\in [1,n]}||x-a^{(i)}|{|}_2$$

위에 개념을 바탕으로 필터 전체에서 흔한 정보(common infromation)을 확보하기 위한 geometric median $F_i^{GM}$은 하나의 $i_{th}$ 레이어에서 다음과 같이 구할 수 있다:

$$F_i^{GM}\in \underset{x\in {\mathbb{R}}^{N_i\times K\times K}}{\mathrm{argmin}}g(x)$$

이 때,

$$g(x)\stackrel{def}{=}\sum _{j^{\prime }\in [1,N_{i+1}]}||x-F_{i,j^{\prime }}|{|}_2$$

같은 $i_{th}$ layer에서 중심점($x$)과 거리의 합이 최소가 되는 filter를 구해야한다. 따라서:

$$F_{i,j^i}\in \underset{j^{\prime }\in [1,N_{i+1}]}{\mathrm{argmin}}||F_{i,j^i}-F_i^{GM}|{|}_2$$

즉, $F_{i,j^i}$ 필터는 각 layer에서 다른 필터들의 대표가 될 수 있다. 따라서 다른 필터를 제거하더라도 전체 모델에서 적은 악영향을 미친다. 다만, Geometric median을 찾는 것은 쉬운 문제는 아니다. 예를들어 간단한 나무 막대에서도 중심점을 찾는 것은 많은 시도를 통해서 얻을 수 있기 때문이다. 이 공간 자체가 무한대라면, 즉 포인트($a^{(i)}$)가 무한이 많이 존재한다면 사실상 중심점을 찾는것은 거의 불가능하다. 하지만 우리는 이미 알고있는 유한 갯수의 filter 집단에서 하나를 선정하기 때문에 위의 문제를 약화 할 수 있다. 우리가 찾는 중심 필터($F_{i,j^i}$)가 Geometric median($F_i^{GM}$)이라는 가정을 한다면 아래와 같다:

$$||F_{i,j^{\ast }}-F_i^{GM}|{|}_2=0$$

그러면 위의 식을 아래와 같이 바꿀 수 있다.

$$F_{i,j^i}\in \underset{j^i\in [1,N_{i+1}]}{\mathrm{argmin}}\sum _{j^{\prime }\in [1,N_{i+1}]}||x-F_{i,j^{\prime }}|{|}_2$$

$$=\underset{j^{\ast }\in [1,N_{i+1}]}{\mathrm{argmin}}g(x)$$

즉, 제거하고자 하는 필터 선택된 필터($F_{i,j^i}$)는 Uclidean distance의 합이 최소화되는 값으로 구할 수 있다. 예를들어 필터 세개의 uclidean 거리가 각각 [0.2, 1, 2, 5]라고 하고, 50% pruning을 진행한다고 하면, minimize를 위해 거리가 먼 2, 5를 삭제하는 방식이다. 여기서 주목해야 할 점은 혹시라도 중심 필터($F_{i,j^i}$)가 제거되어야 하는 경우라도 여전히 Geometric median을 구하는 식은 동일하다.

$$F_{i,j^{i^{\prime }}}\in \underset{j^i\in [1,N_{i+1}]}{\mathrm{argmin}}{g}^{\prime }(x)$$

이때,

$$g^{\prime }(x)=\sum _{j^{\prime }\in [1,N_{i+1}],j^{\prime }\ne j^{\ast }}||x-F_{i,j^{\prime }}|{|}_2$$

이는 전체 $g(x)$함수에서 특정 필터를 제거하는 것임으로,

$$g^{\prime }(x)=g(x)-\sum _{j^{\prime }=j^{\ast }}||x-F_{i,j^{\prime }}|{|}_2$$

$$=g(x)-||x-F_{i,j\ast }|{|}_2$$

위와 같이 나타 낼 수 있고, 이를 minimize 하면

$$\min g^{\prime }(x)=\min g(x)-||x-F_{i,j\ast }|{|}_2$$

$$=\min g(x)-\min ||x-F_{i,j^{\ast }}|{|}_2$$

$$=g(F_{i,j^i})-\min ||x-F_{i,j^i}|{|}_2$$

우리는 $x$가 $F_{i,j^{\ast }}$라고 가정했기 때문에 결국엔

$$F_{i,j^{i^{\prime }}}=F_{i,j^i},since||x-F_{i,j^{{}^{\prime }}}|{|}_2=0$$

필터가 제거되더라도 Geometric Median 값은 영향이 없다는 것을 알 수 있다.

논문에서 제시한 FPGM 알고리즘은 아래와 같다.

논문에 제시한 알고리즘에는 잘 나타나와 있지 않지만, 아이디어를 구현한 소스코드를 보면 먼저 전체 필터에서 norm이 큰 후보군을 먼저 뽑는다. 이후, 이 후보군들을 바탕으로 GM을 구하고 제거하는 형태다.

구현체에서 Uclidean distance를 구하기 위해 scipy.spartial 모듈의 distance 함수를 사용했는데, 이는 구현의 편의상 이렇게 활용한것으로 보인다. Euclidean distance PyTorch로 구현하게 되면 이중 for문을 활용함으로써 복잡하다고 생각한듯하다.

Numpy의 argsort() 함수를 사용하면 내림차순으로 정렬함으로 Uclidean distance가 작은 수 순서대로 정렬을 진행한다. 즉, 비슷한 순서대로 정렬을 한다. 비슷하지 않는 필터, $F_{i,j^{\ast }}$를 최소화하기 위한 필터들의 index 번호를 바탕으로 weight 0으로 바꿈으로써 pruning을 진행한다.

3. Experiments

실험은 single-branch network인 VGGNet과 multiple-branch network인 ResNet 사용했다. 데이터는 Cifar-10과 ILSVRC-2012를 활용했다.

3.1 Single-Branch Network Pruning

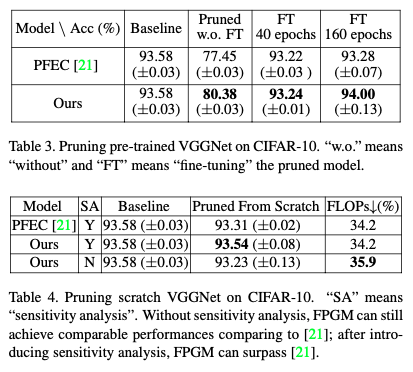
Pretrained된 모델과 처음부터 학습한 결과다. 근소하지만 기존의 방법보다 약간 성능향상을 보였다.

3.2 Multiple-Branch Network Pruning

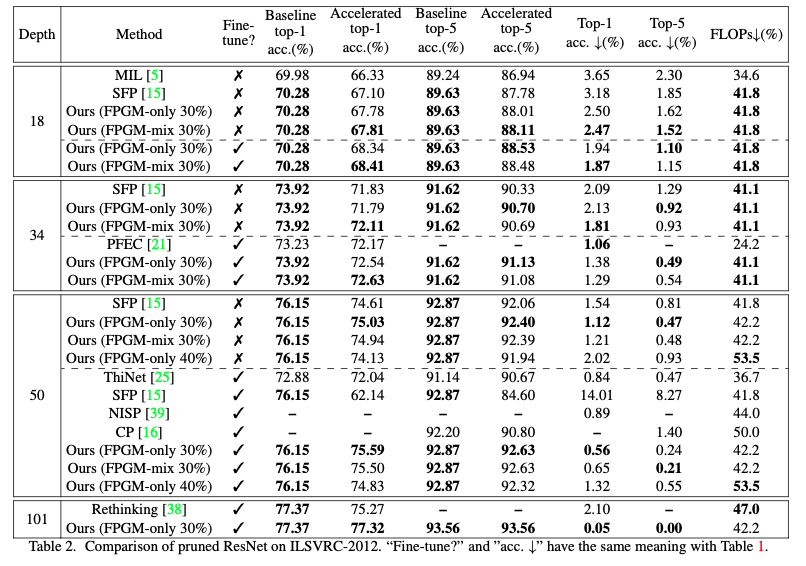
오히려 ResNet에서 더 좋은 결과를 보이는 것으로 확인된다. Accuracy drop도 적으면서, FLOPS는 크게 낮췄다. 이는 ILSVRC-2012 데이터에서도 나타난다.

(필자 개인의견)여기서 SFP는 동일한 저자들이 GM을 고려하지않고 Large norm filter만 제거한 논문인데, 다소 아쉬운 것은 SFP와 성능 차이가 크지 않다는 점이다. 물론 ResNet-50에서는 FLOPS를 크게 늘리긴했다. Depth가 낮은 모델에서는 FPGM이 크게 활용되기 어려울 수도 있다.

4. Conclusion

본 논문에서는 Filter pruning 연구에서 “smaller-norm-less-imortant” 기준에 의문점을 가지면서 1) norm deviation이 충분히 커야한다는 것과 2)norm이 0에 충분히 가까워야한다는 두가지 조건을 언급했다. 하지만 현실에서는 충족하지 못할 수 있는 조건이기 때문에 Geometric Median 값을 바탕으로 Most replaceable contribution filter를 제거하는 방법을 제시한다. 기존 방법론들에 비해 accuracy의 향상은 미미했으나, FLOPS를 줄일 수 있었고, 특히 깊은 모델에서 그 효과가 더 잘 나타는것을 보여줬다. 그럼에도 불구하고 단순히 norm값을 계산하는 방법에 추가적인 방법이 더해져야하는 상황에서 본 방법론을 활용할 가치가 있는지 고민이 더 필요해보인다.