Regularization-L1 and L2 Norm
1. Regularization
기계학습에서 일반적으로 regularization은 학습 모델이 데이터에 너무 fit하게 학습하는 경우, 즉 과적합(overfitting)이 발생하는 경우에 일반성을 부여하기 위해 사용한다. [그림 1]에서 Underfitting하는 경우에는 아직 결정경계가 두개의 클래스를 다 분류하기에 부족하게 학습이 진행되었다. 반면, Overfitting 케이스에서는 결정경계가 너무 과도하게 학습 데이터에 맞춰서 학습이 되었다. 이러한 경우, 학습 데이터에서 accuracy가 높더라도, 테스트 데이터에서는 accuracy가 낮게 나올 수 있다. 따라서 이런 현상이 발생한 경우, overfitting을 의심 할 수 있고 모델에 일반성(regularization)을 부여하는 것이 필요하다.
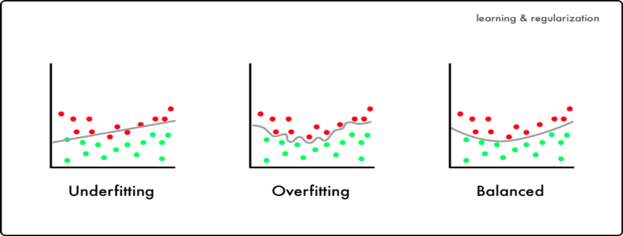
Overfitting을 해결하는 방법은 매우 다양하다. 데이터를 조작 할 수 있고, 모델을 수정 할 수도 있다. 이번 내용에서는 그 중 학습 방법에서 일반성을 부여하는 regularization에 대해 설명하고자 한다. 물론 다양한 형태로 regularization을 할 수 있지만, 이번에는 학습 loss에서 노름(norm)을 활용한 방법을 소개한다.
2. Norm
수학에서, 노름(norm)은 실수 또는 복소수 벡터 공간에서 원점으로부터의 거리와 같은 특정한 방식으로 측정하는 음이 아닌 실수값을 갖는 함수다[1]. 즉, 벡터의 크기(강도, 길이)의 척도를 나타내는 수학적인 용어다[2]. 일명 Manhattan norm이라고 불려지는 L1 norm은 두 벡터 사이의 모든 성분의 절대값의 합으로 나타낼 수 있다. 벡터의 크기를 측정 할 때 가장 흔하게 사용하는 Euclid norm의 경우는 원점에서 특정 벡터까지의 직성 거리를 측정한다. 그리고 Norm은 아래와 같은 식으로 일반화 할 수 있다. 이를 P-Norm이라 한다.
$$
||\boldsymbol{x}||_p= \left( \sum ^n_{i=1}|x_i|^p \right)^{1/p}
$$
이때, P가 1이라면 L1 norm을 의미하고, p가 2라면 L2 norm을 의미한다.
(1) L1 Norm
L1 norm은 위의 정의에 따라서 벡터의 모든 성분의 절대값의 합으로 나타낼 수 있다.
$$
||\boldsymbol{x}||_1=\sum^n_{i+1}|x_i|
$$
이는 아래 [그림2]과 같이 원점으로부터 벡터의 좌표를 측정 할 때, 성분의 합으로 나타 낼 수 있다.
예를 들어 한 블럭을 1의 크기로 가정 할 경우, $||\boldsymbol{x}||_1=|2|+|3|=5$ 와 같이 계산 할 수 있다 [3].

(2) L2 Norm
반면, L2 Norm은 출발점에서 도착점까지의 거리를 직선거리로 측정한다([그림3]). L2 Norm은 P-norm 정의에 의해 다음과 같이 정의 할 수 있고, 이를 흔히 알고있는 유클리드 norm이라고 말한다.
$$
||\boldsymbol{x}||_2=\left(\sum^n_{i+1}|x_i|^2\right)^{1/2}=\sqrt{\sum^n_{i+1}|x_i|^2}
$$
마찬가지로 블럭 하나를 1의 크기라고 가정할 때, 유클리드 norm은 다음과 같이 계산 할 수 있다[3].
$||\boldsymbol{x}||_2=\sqrt{2^2+3^2} = \sqrt{13}$

(3) Norm with constraint
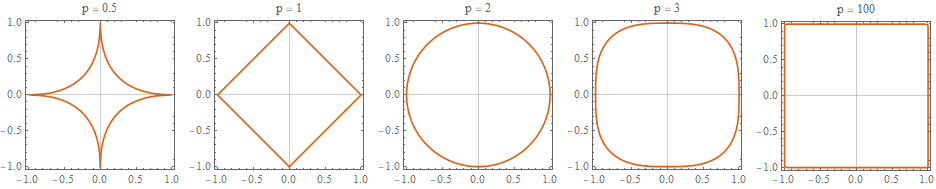
Norm에 제약(constraint)를 부여하면 p값에 따라 Norm의 각기 다른 모양의 그래프를 볼 수 있다. 아래 [그림 4]은 p값에 따른 constraint 1에서의 norm 그래프를 나타낸 것이다. 즉, $||\boldsymbol x||_p = 1$.
P 값이 커질 수록 사각형 모양에 가까워지는 것을 알 수 있다. 기계학습에서 흔하게 사용하는 L1, L2 norm은 각각 다이아몬드 모양과 원 모양의 함수를 나타낸다. Norm의 그래프 모양은 regularization에서 sparsity를 부여하는 중요한 요소이다.
3. Norm in Machine Learning regularization
앞서 언급했듯, 기계학습에서는 norm을 regularization에 활용하고있다. 필자는 norm이 loss 함수에서 어떻게 regularization 효과를 일으키는지 수학적으로 설명하기 어렵기 때문에 그림을 통해 직관적으로 설명하고자한다.
(1) Balancing the error between the regularization term
기본적으로 norm regularization은 loss 함수에 패널티를 주는 방식으로 적용한다. 여기서 DataLoss는 데이터로부터 얻을 구하는 loss 함수를 의미한다. 보통 CrossEntropy loss나, MSE 등이 될 수 있다. 여기에 norm 값을 부여하는 방식으로 regularization을 수행한다. 이 때, 수식에서 볼 수 있듯이 norm term은 데이터와 독립적이며 파라미터의 거리를 줄이는 것(variance)에 목적을 둔다.
$$ Loss(\theta, x) = DataLoss(\theta, x) + \lambda||\boldsymbol \theta ||_p $$
그럼 Loss 함수를 구성함에 있어서 L1, L2 norm을 패널티로 부여했을때 어떻게 동작하는지 확인해보도록하자. 앞서 언급했든 수학적으로 미분을 통해 설명하면 더 정확히 이해 가능하겠지만, 필자는 그래프를 통해 직관적으로 이해를 돕고자한다.

위 [그림 5]는 Data loss 함수(빨간색 타원)와 L1과 L2 norm의 그래프(민트색 그래프 영역)를 나타내고있다. 이해를 쉽게 하기위해 파라미터($\beta_1, \beta_2$)가 두 개만 존재하는 2차원 평면으로 제한한다. Data loss 값에서 $\hat{\beta}$ 은 data loss에서 최소값을 의미한다. 빨간색 타원들은 loss의 범위를 의미하는데, $\hat{\beta}$에 가까워질수록 데이터에 따른 오차가 줄어드는 것으로 이해 할 수 있다. Overfitting은 학습 모델이 $\hat{\beta}$에 너무 가까워지는 현상에 의해 발생함으로 일반성을 부여하기 위해 ‘어느정도’ loss를 감수 할 수 있도록 모델을 유도해야한다.
여기서 ‘어느정도’라는 모호한 기준을 명확(clarify)하게 하기 위해 norm을 활용한다. Optimization은 위에서 제시한 전체 loss가 0으로 되는 것을 목표로 진행된다. $Loss(\theta,x)$가 0이라고 가정하면, 아래와 같이 나타 낼 수 있다.
$$0=DataLoss(\theta,x) + \lambda||\theta||_p$$
Norm은 데이터에 대해서 독립적이기 때문에 $\theta$ 기준으로 방정식을 구할 수 있다. 이때의 해는 DataLoss 함수와 Norm의 접점이 된다. 따라서 [그림5]와 같이 Norm 그래프의 최대 거리에 인접하는 DataLoss 값이 해가 된다. 이로 인해 데이터를 바탕으로 구해지는 loss가 $\hat{\beta}$에 너무 가까워 지는 것을 방지 할 수 있다.
(2) L1 vs L2 Norm
L1 norm과 L2 norm은 어떤 차이가 있을까? L1 norm은 다이아몬드 형태의 그래프를 나타내고 있고, L2 norm은 원 형태의 모양을 갖는다. 이러한 모양 차이(geographical difference)에 의해서 L1은 모델의 loss가 axis위에 인접하는 결과를 얻을 수 있다[5]. [그림 5]에서 보면, 두 DataLoss 함수의 위치는 동일하지만, L1 norm의 경우에는 모양의 특성에 의해 Axis와 교점이 생기는 것을 알 수 있다. 반면, L2 norm은 그렇지 않다. L2가 Axis와 교점이 생기는 경우는 $\hat{\beta}$ 또한 Axis 위에 있을 경우를 의미하는데, $\hat{\beta}$ 이 특정 $\theta$값 위에 존대한다는것은 모델(e.g., $f(x) = \theta_1 X+\theta_2X$)에서 ‘항상 데이터의 특징을 전혀 반영하지 않는다’는 것이기 때문에 사실상 해가 될 수 없다.
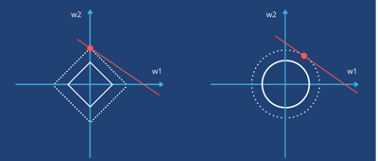
Geographical difference에 의해 발생하는 예시는 위 [그림 6]에서도 잘 나타난다. 빨간색 선이 DataLoss라고 정의 가정한다면, L1 Norm 그래프의 경우에는 norm의 constraint를 키우거나 죽이는 방식으로 Axis에 해가 존재 할 수 있다. 반면, L2 norm 그래프의 경우에는 axis위에 인접하는 결과를 얻기 어렵다.
(3) Sparsity on L1 Norm
그렇다면, “Axis에 인접한 결과를 얻는다”는 것이 무슨 의미일까? 이는 곧 파라미터가 sparse 하다는 것을 의미한다. 위 [그림 6]에서처럼 교점의 해가 $(w_2,0)$와 같은 case가 발생한다. 이는 곧 w2의 정보는 살리고, w1의 입력으로 들어오는 결과는 제거하는 효과를 나타낸다. 여기서 위에 언급한 $\hat{\beta}$ 가 Axis위에 존재하는 것과는 전혀 다른 의미다. Norm은 데이터와 독립적이기 때문에 norm과 DataLoss 함수의 해가 $(w_2,0)$ 를 갖는다 하더라도, 그것이 곧 DataLoss의 minal point $\hat{\beta}$ 가 Axis위에 있는 것을 말하고 있지 않기 때문이다. 이에 대한 수학적인 해설이 필요한 경우라면 레퍼런스 [6]을 참고하는 것을 추천한다.
결론적으로는 기계학습 학습에 있어서 parameter에 sparsity를 부여하고 싶다면 L1 regularization을 활용하는 것을 검토 해볼 수 있고, 데이터 손실이 많이 발생하는 것을 피하고 싶다면 L2 regularization을 활용하는 것이 좋다.
4. 정리
- Regularization은 Overfitting을 해결하는게 많이 사용하는 방법이다.
- Regularization은 L1, L2 norm을 사용하는 방법이 존재한다.
- Data Loss와 Norm 간에 balancing을 통해 data loss가 minmal point에 fit하는 것을 방지한다.
- L1 norm은 sparsity를 부여 할 수 있다.
References
[1] “Norm”, https://en.wikipedia.org/wiki/Norm_(mathematics), last accessed at Nov. 14. 2022
[2] 정보통신기술용어해설, “Norm”, http://www.ktword.co.kr/test/view/view.php?m_temp1=4201, last accessed at Nov. 14. 2022
[3] “놈(Norm)이란 무엇인가?”, https://bskyvision.com/entry/선형대수학-놈norm이란-무엇인가, last accessed at Nov. 14. 2022
[4] Alexander Ihler, “Linear regression (6): Regularization”, https://youtu.be/sO4ZirJh9ds, last accessed at Nov. 15. 2022
[5] Steve Bruton, “Sparsity and the L1 Norm”, https://youtu.be/76B5cMEZA4Y, last accessed at Nov. 15. 2022
[6] Anand Seetharam, “L1 and L2 Regularization”, https://youtu.be/QNxNCgtWSaY, last accessed at Nov. 15. 2022